Understanding fractions is one of the most exciting and useful sets of lessons in grade school mathematics. The creator of this website is thrilled that you visited this page, you, young achiever! You might be a grade 4 student or a bit older, right now! If you are, you have come to the right place. If you’re a bit younger, perhaps you need assistance from an older brother or sister. But hey, who am I to underestimate you, achiever? You might find the presentation of the lessons here a bit messy. That’s my kind of math – unpolished, raw, a work in progress, and a bit messy! And that’s ok! We are all a work in progress anyway! Let us explore and have fun together!
Do NOT answer this yet. After the last lesson on this page, there’ll be a quiz about this.
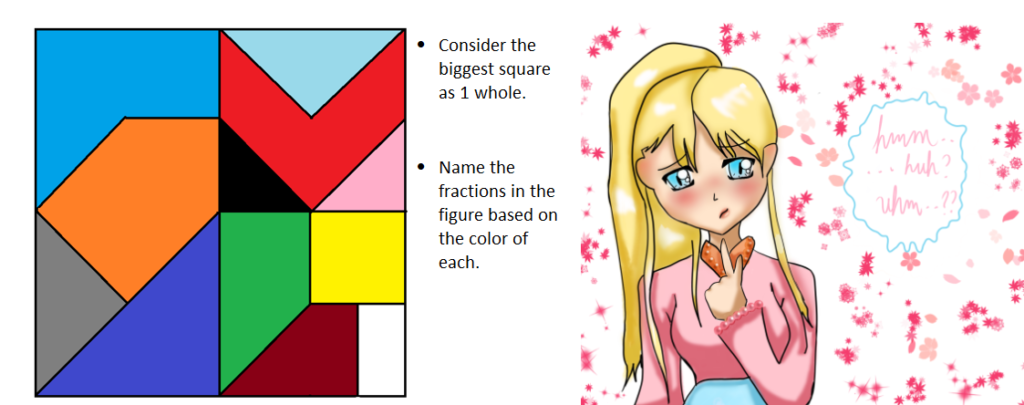
- 1. What are fractions?
- 2. What does a fraction look like?
- 3. When is a fraction a proper fraction? an improper fraction?
- 4. What are equivalent fractions? How else can an improper fraction be written?
- 5. How are equivalent fractions generated?
- 6. How do we add similar fractions? How do we apply the concept of equivalent fractions in simplifying fractions?
- 7. How do we add or subtract similar fractions? dissimilar fractions?
- Review all the videos on this page in one go (optional)
1. What are fractions?
Activity
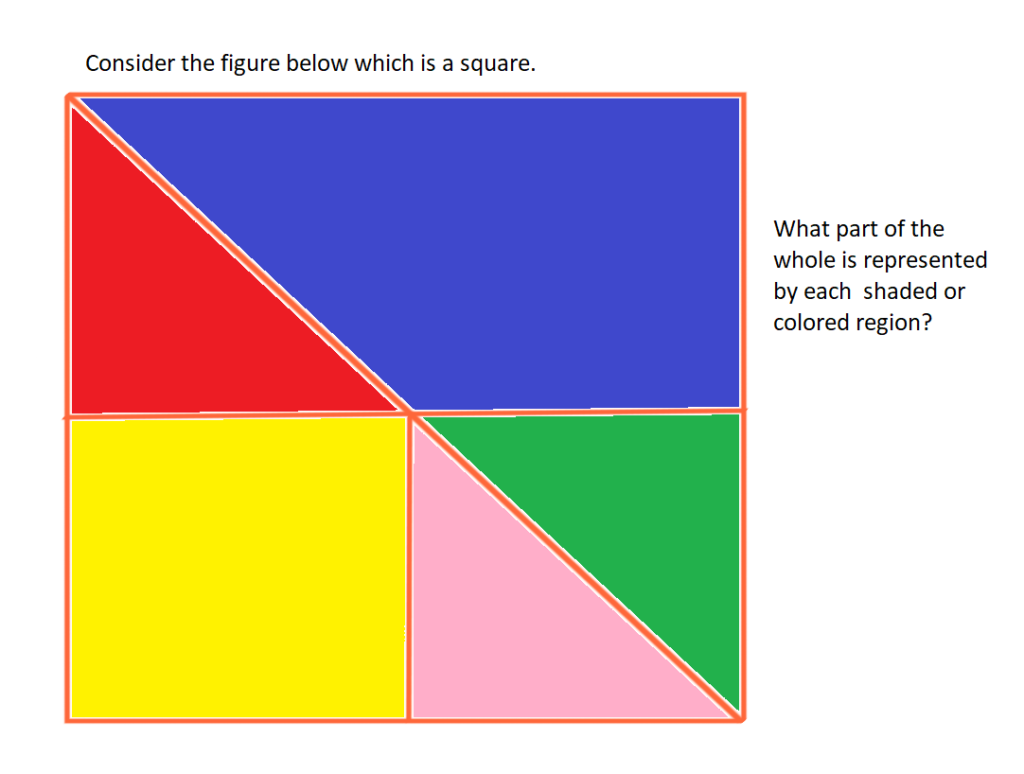
Click the video on the right side if you need further explanation.
Test yourself 1!
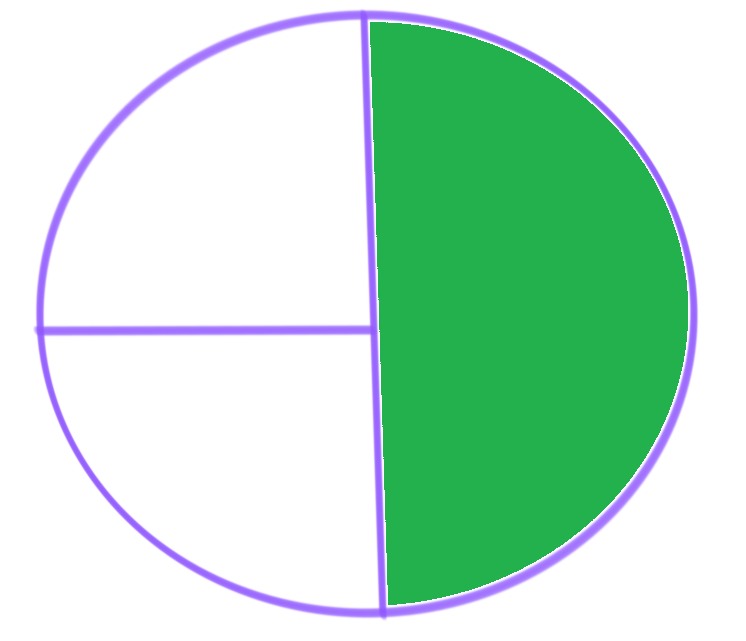
Test yourself 2!
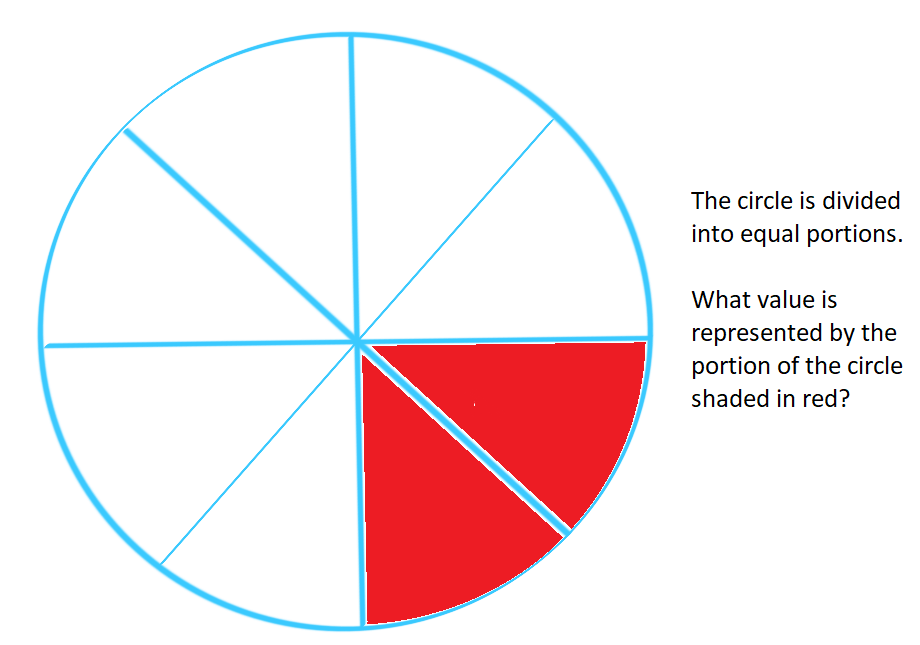
Test Yourself 3!
Summary
Fractions may be used to name part of a whole figure or part of an equally spaced number line.
If a figure is equally divided, naming parts of that figure is easy. If a whole is divided into two equal parts, each part is 1/2.
If a whole is divided into 3 equal parts, two parts of that figure equals 2/3 of that figure.
A whole that is equally divided into 7 regions, for example, has 1/7 for each small portion or region of that figure.
The challenge, most of the time, in naming the fraction that represents the shaded or the colored region is to figure out how the figure is divided into EQUAL parts.
References
2. What does a fraction look like?
Activity and Lesson Proper
Here is the same video that you can play once without pauses. If you have done the activity above though, you don’t need to watch the same video again.
Test Yourself 1!
Test Yourself 2!
Summary
References
3. When is a fraction a proper fraction? an improper fraction?
Activity
Test Yourself 1!
Test Yourself 2!
Summary
The numerator of a fraction refers to the number of parts being considered.
The denominator of a fraction refers to the total number of equal parts the whole is divided into.
For example, 3/8 means three “one-eighths”. 3 parts are being considered in a whole that is divided into 8 equal parts.
Provided that the fraction is a positive number, if the numerator is less than the denominator, the fraction is called a proper fraction. The value of a proper fraction is less than 1.
Provided that the fraction is a positive number, if the numerator is equal to or greater than its denominator, the fraction is called an improper fraction and its value is either equal to or greater than 1.
Note that in the entirety of the lessons on this page, unless otherwise stated, the fraction being referred to is positive.
References
4. What are equivalent fractions? How else can an improper fraction be written?
Here we illustrate equivalent fractions using two congruent objects representing wholes and using the number line.
Activity
Test Yourself 1!
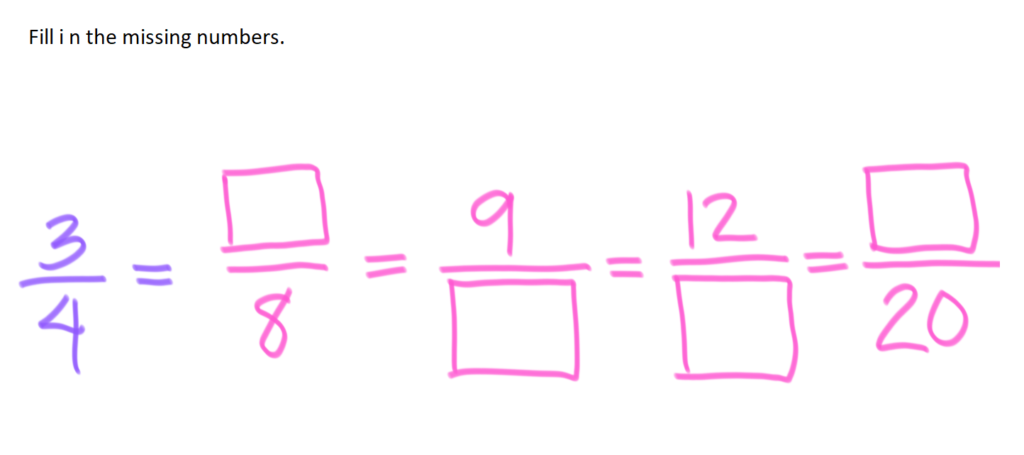
Test Yourself 2!
Summary
References
5. How are equivalent fractions generated?
Activity
Test Yourself
Summary
How are equivalent fractions generated?
We may multiply the numerator and the denominator of a fraction by the SAME number. The resulting fraction and the original fractions are equivalent fractions.
If the numerator and the denominator of a fraction are both divisible by the SAME number other than 1, dividing the numerator and the denominator of that fraction will produce another fraction in simpler form. The resulting fraction and the original fraction are equivalent fractions. (Note that dividing the numerator and the denominator of that fraction by their greatest common factor (GCF) will produce another fraction in its simplest form. – There will be a clearer explanation of this in the next lesson.)
References
6. How do we add similar fractions? How do we apply the concept of equivalent fractions in simplifying fractions?
Here is the 1st lesson in adding fractions – adding fractions that have the same denominator.
Here, we’ll learn more about adding similar fractions and reducing or simplifying fractions.
Activity
Test Yourself
If you wish to see the solution, watch the video below:
If you wish to see the solution, watch the video below:
If you wish to see the solution, watch the video below:
Summary
References
7. How do we add or subtract similar fractions? dissimilar fractions?
Activity
Here is a drag-and-drop activity for you.
Test Yourself 1!
Do you need further explanation? If you did not get the above item correctly, here is another example.
Test Yourself 2!
Summary
In adding similar fractions, add the numerators and copy the same denominator. Simplify or express your final answer in its simplest form.
In adding dissimilar fractions, convert the addends into similar fractions. You may do this by multiplying the numerator and the denominator of each of the addend fractions by the LCD of the fractions.
After renaming the dissimilar fractions and making them similar fractions, follow the rules in adding similar fractions. Again, simplify.
References
You are now ready to take the quiz.

Quiz proper: Here is a drag-and-drop quiz for you! Express your answer in the simplest form. Good luck!
Review all the videos on this page in one go (optional)
- 1. What are fractions?
- 2. What does a fraction look like?
- 3. When is a fraction a proper fraction? an improper fraction?
- 4. What are equivalent fractions? How else can an improper fraction be written?
- 5. How are equivalent fractions generated?
- 6. How do we add similar fractions? How do we apply the concept of equivalent fractions in simplifying fractions?
- 7. How do we add or subtract similar fractions? dissimilar fractions?
- Review all the videos on this page in one go (optional)
Leave a Reply